周期结构中连续谱中的束缚态

报告题目：周期结构中连续谱中的束缚态

报 告 人：袁利军 教授（重庆工商大学）

时    间：2020年6月23日（周二）15:30-17:30

地    点：腾讯会议，会议号：872635798

邀 请 人：韩德专

报告摘要：

Talk 1: 周期结构中连续谱中的束缚态：数学理论和数值计算

Abstract：A bound state in the continuum (BIC) is a localized eigenmode that does not couple with compatible waves propagating to or from infinity. For photonic systems, a periodic structure sandwiched between two homogeneous media is the most popular platform for observing BICs and realizing their applications. Since a BIC can be regarded as a resonant state with an infinite quality factor, it is possible to realize resonant states with extremely high quality factors by perturbing the structures or varying the Bloch wavevector. Due to their unusual properties, the BICs are useful in a number of applications. In this talk, I will present the basic mathematical theory and numerical computations of the BICs on periodic structures.

Talk 2: 周期结构中连续谱中的束缚态：鲁棒性、场增强和非线性应用

Abstract: A BIC is robust if the original structure is slightly changed, the original BIC is simply shifted to a new one with a slightly different frequency and wave vector. Near a BIC on periodic structures, resonant modes with large high quality factor can be realized by varying the Bloch wavevector or perturbing the structures. Typically, the quality factors are proportional to 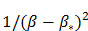 or , where 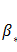 is the Bloch wavevector of the BIC and  is the amplitude of the structure perturbation. 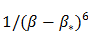Our researches indicate that the quality factors can be  or 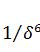 near some special BICs.  Therefore, large field enhancement can be realized near these BICs.  In this talk, I will present our recent researches about the robustness, field enhancement and nonlinear application of BICs.

报告人简介：

袁利军，重庆工商大学教授。2010年毕业于香港城市大学数学系，获得计算数学博士学位。目前主要从事光波和微纳光子结构的数学理论、模型和数值计算方面的研究，主持国家自然科学青年基金1项，重庆市自然科学基金2项，在SIAM J. Appl. Math.、J. Comput. Phys.、Phys. Rev. A等杂志发表SCI论文近30篇。